ข้อสอบ GMAT Math พร้อมเฉลย มาทดสอบกันพร้อมสอบแค่ไหน?

1. Set T is a finite set of positive consecutive multiples of 14. How many of these integers are also multiples of 21?

(1)Set T consists of 30 integers.
(2)The smallest integer in Set T is a multiple of 21.

EACH statement ALONE is sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

2. IF $yz ≠ 0$ , is $\displaystyle \frac{x-y+z}{2z}< \frac{x}{2z}-\frac{y}{2z}-\frac{x}{y}?$

(1) $\displaystyle \frac{x}{y}< -\frac{1}{2}$
(2) $\displaystyle xy< 0$

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

EACH statement ALONE is sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

3. Is $\displaystyle x>9$ ?

(1) $\displaystyle x^2+3x=28$
(2) $\displaystyle 9x=5x-28$

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

EACH statement ALONE is sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

4. A beer company spent $100,000 last year on hops, yeast, and malt. How much of the total expenditure was for hops?

(1)The expenditure for yeast was 20% greater than the expenditure for malt.
(2)The total expenditure for yeast and malt was equal to the expenditure for hops.

EACH statement ALONE is sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

5. What is the value of j+k?

(1) mj + mk = 2m
(2) 5j + 5k = 10

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked.

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

6. x is a positive integer less than 20. What is the value of x?

(1) x is the sum of two consecutive integers.
(2) x is the sum of five consecutive integers.

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

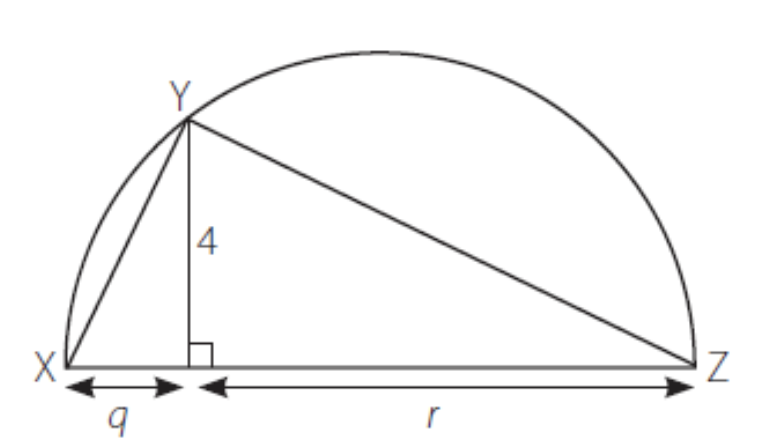
7.If arc XYZ above is a semicircle, what is its length?

(1) q = 2
(2) r = 8

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

8.What is the value of x?

(1)(x)(x + 1) = (2013)(2014)
(2)x is odd

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

9.If Alyssa is twice as old as Brandon, by how many years is Brandon older than Clara?

(1)Four years ago, Alyssa was twice as old as Clara is now.
(2)Alyssa is 8 years older than Clara.

EACH statement ALONE is sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

10.In the first hour of a bake sale, students sold either chocolate chip cookies, which sold for $1.30, or brownies, which sold for $1.50. What was the ratio of chocolate chip cookies sold to brownies sold during that hour?

(1)The average price for the items sold during that hour was $1.42
(2)The total price for all items sold during that hour was $14.20

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

11. If $a, b,$ and $c$ are distinct positive integers where $a<b<c$ and $\displaystyle \sqrt{abc}=c$ what is the value of $a$ ?

(1) $c$ =8
(2) The average of $a,b,$ and $c$ is $\displaystyle \frac{14}{3}$

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

EACH statement ALONE is sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

12. Line M is tangent to a circle, which is centered on point (3, 4). Does Line M run through point (6, 6)?

(1) Line M runs through point (-8, 6)
(2) Line M is tangent to the circle at point (3, 6)

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

EACH statement ALONE is sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

13. For nonnegative integers $x$ and $y$ , what is the remainder when $x$ is divided by $y$ ?

(1) $\frac{x}{y}$ =13.8
(2) The numbers $x and y$ have a combined total of less than 5 digits.

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

EACH statement ALONE is sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

14. If $x$ and $y$ are positive integers, is $xy$ an integer?

(1) Every factor of $y$ is also a factor of $x$
(2) Every factor of $x$ is also a factor of $y$

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

15. What is the average of the terms in set J?

(1) The sum of any three terms in Set J is 21
(2) Set J consists of 12 total terms.

EACH statement ALONE is sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

16. Is xy > 24?

(1) y - 2 < x
(2) 2y > x + 8

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

EACH statement ALONE is sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

17. If $xy≠0$ , is $\displaystyle \frac{1}{x}+\frac{1}{y}=16?$

(1) $\displaystyle x+y=16xy$
(2) $\displaystyle x=y$

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

18. What is the value of $x+2y$ ?

(1) $\displaystyle 3^x9^y=27^12$
(2) $\displaystyle x=2y$

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked

19. Is $\displaystyle a^2>3a-b^4?$

(1) $\displaystyle 3a-b^4=-5$
(2) $\displaystyle a>5$ and $\displaystyle b>0$

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

EACH statement ALONE is sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

20. If $\displaystyle xy\neq 0$ , is $\displaystyle a>\frac{y}{x}?$

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

EACH statement ALONE is sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

21. What is the value of two-digit integer x?

(1) The product of the two digits is 14.
(2) x is divisible by 9.

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

EACH statement ALONE is sufficient to answer the question asked

22. In a retail store, the average (arithmetic mean) sale for month M was d dollars. Was the average (arithmetic mean) sale for month J at least 20 percent higher than that for month M?

(1) For month M, total revenue from sales was $3,500.
(2) For month J, total revenue from sales was $6,000.

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

23. (NOTE: not drawn to scale) Is a > 85?

(1) b > 75
(2) c > 95

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

EACH statement ALONE is sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

24. Is a>b−c?

(1) c>b−a
(2) b

EACH statement ALONE is sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

25. Is $\displaystyle x>6?$

(1) $\displaystyle x^2=49$
(2) $\displaystyle 7x=x^2$

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

26. 3,8,a,17,b If b=3a, is the average (arithmetic mean) of the five terms in the list above less than 8?

(1) a>2
(2) a²<9

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

27. Is $\displaystyle p^3< p?$

(1) p<1
(2) p is an integer

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

EACH statement ALONE is sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

28. Is the area of circular region X greater than the area of circular region Y?

(1) The circumference of circle X is greater than the circumference of circle Z, and the circumference of circle Z is less than the circumference of circle Y.
(2) The radius of circle X is greater than the radius of circle Y.

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

EACH statement ALONE is sufficient to answer the question asked

29. An artist's portfolio consisting of 1,000 photos is divided into 20 subjects. After an extensive photo shoot, two more subjects are then added to the portfolio. Is the average (arithmetic mean) number of photos in each subject greater than 55?

(1) Each of the new subjects has fewer than 117 photos.
(2) Each of the new subjects has more than 71 photos.

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

EACH statement ALONE is sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

30. Jeff’s average (arithmetic mean) monthly utility bill for the months of June, July, and August was $75. During which month did he receive the highest bill?

(1) The lowest bill was received in July.
(2) The total of his bills for July and August was $160.

EACH statement ALONE is sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

31. A certain company paid bonuses of $125 to each of its executive employees and $75 to each of its non-executive employees. If 100 of the employees were non-executives, how many of the employees were executives?

(1) The company has a total of 120 employees.
(2) The total amount that the company paid in bonuses to its employees was $10,000.

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

EACH statement ALONE is sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

32. A certain jewelry store sells gold necklaces in 18-inch and 28-inch lengths, and all necklaces of the same length sell for the same price per necklace regardless of the number of necklaces purchased. What is the price of a 28-inch necklace at this jewelry store?

(1) The total price of an 18-inch and a 28-inch gold necklace is $68.
(2) The total price of two 18-inch necklaces and one 28-inch necklace is $96.

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

EACH statement ALONE is sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

33. For integers $\displaystyle a,b,$ and $c$ , $\displaystyle \frac{a}{(b-c)}=1$ .What is the value of $\displaystyle \frac{(b-c)}{c}?$

(1) $\displaystyle \frac{a}{b}=\frac{3}{5}$
(2) $\displaystyle a$ and $\displaystyle b$ have no common factors greater than 1.

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

34. By how many years is Jason older than Allison?

(1) Jason is 6 years older than twice David’s age.
(2) In 8 years, Allison will be twice as old as David is now.

EACH statement ALONE is sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

35. Exactly how many show dogs does Sheila have?

(1) Of Sheila’s show dogs, exactly 3 have won prizes of at least $500.
(2) Of Sheila’s show dogs, exactly 40% have not won a prize of $500 or more.

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

EACH statement ALONE is sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

36. Julie runs a small art museum. How many paintings does her museum have?

(1) Her next acquisition of 4 Monet paintings will increase the number of paintings in the museum’s collection by 10%
(2) The museum currently exhibits 3 impressionist paintings for every 2 non-impressionist paintings.

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

EACH statement ALONE is sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

37. A bake sale sells only individual cupcakes and boxes of cookies. If cupcakes sell for $2 each, and a box of cookies sells for $15, how many boxes of cookies did Kevin buy?

(1) Kevin spent $27
(2) Kevin bought 6 cupcakes

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked

Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

EACH statement ALONE is sufficient to answer the question asked

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked