ข้อสอบ CU-AAT Math วิชาคณิตศาสตร์ อินเตอร์ จุฬา พร้อมเฉลย
CU AAT MATH
1. If every digit of a whole number is either a 5 or 7, the number must be
2. If 3a - 6 = 15, then what is the value of 3(10 - a)?
3. If 1 hexaminute is equivalent to 6 minutes of time, how many hexaminutes are equivalent to 5 hours of time?
4. If it takes Ann 10 hours working at a constant rate to complete her science project, what part of the project is completed in 6 hours?
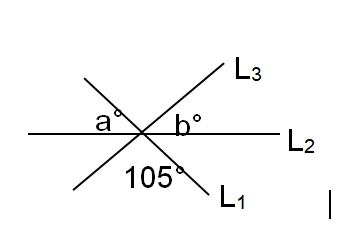
5. Three lines intersect in the figure above. What is the value of a + b?
6. Which of the following groups contains three fractions that are equal?
7. Bob buys a book and a pen for 18 baht. If the book costs 3 baht more than the pen,
how much the pen cost in baht?
how much the pen cost in baht?
8. “If a and b are integers and b ≠ 0 then \frac{a}{b} is an integer.”
Which of the following value of a and b proves that the statement above is not true?
Which of the following value of a and b proves that the statement above is not true?
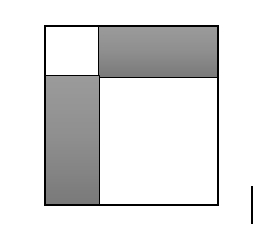
9. In the figure above, the large square is divided into two smaller squares and two shaded rectangles. If the perimeter of the two smaller squares are 8 and 20, what is the sum of the area of the two shaded rectangles?
10. Which of the following represents the largest value?
11. For which of the following sets of numbers is the average(arithmetic mean) greater than the median?
12. At a party there are M men and W women. If 4 more men arrive, and 3 women leave, what fraction of the party are now women?
13. 70 percent of 90 is the same as 60 percent of what number?
14. Note: Figure not drawn to scale.
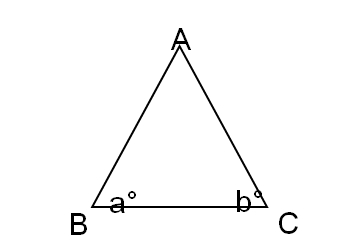
In ∆ ABC above, if a < b, which of the following must be true?
In ∆ ABC above, if a < b, which of the following must be true?
Let ∇n be defined for any positive integer n as the number obtained by writing the digits of n in reverse order, dropping any leading zero that result.
For example, ∇3 = 3, ∇30 = 3, and ∇321 = 123.
15. What is the value of ∇36,000 - ∇32,000 ?
For example, ∇3 = 3, ∇30 = 3, and ∇321 = 123.
15. What is the value of ∇36,000 - ∇32,000 ?
16. Which of the following is equal to ∇82 + ∇401 ?
17. Which of the following must be true for all positive integer n?
I. ∇ (∇n) = n
II. ∇ (10.n) < 10.n
III. ∇(1 + n) = 1+ ∇n
I. ∇ (∇n) = n
II. ∇ (10.n) < 10.n
III. ∇(1 + n) = 1+ ∇n
18. If x = 3y, y = 4z, w = 6z and w ≠ 0, then \frac{x}{w} =
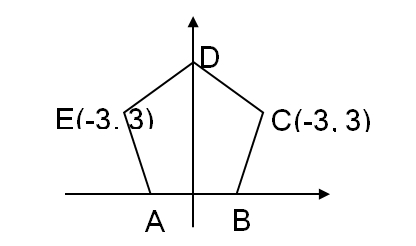
19. In pentagon ABCDE above, how many diagonals with positive slope can be drawn?
20. Which of the following is equal to the sum of two consecutive odd integers?
21. What fraction of 200 is \frac{2}{3} of 120?
22. If a and b are different positive integers, a < b and 3a⋅3b = 81, what is the value of b?
23. If 2 ≤ a ≤ 7 and -2 ≤ b ≤ 3, which of the following is the maximum values of a - b ?
24. In the formula S = 2(w1 + 1h + wh), what is the value of h, in terms of S, w and 1?
25. If one side of a square is increased by 3, and adjacent side is multiplied by 4, the resulting rectangle has a perimeter which is 3 times the perimeter of the original square. What the area of the original square ?
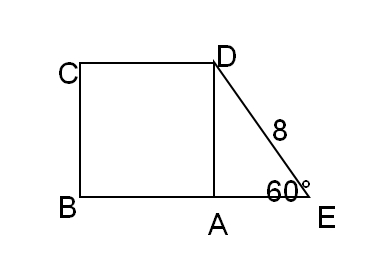
26. In the figure above, ABCD is a square, what is the perimeter of trapezoid BCDE?
27. A boy spends \frac{2}{5} of his money on books and \frac{3}{10} of his money on food. If he is left with 300 baht, how much money did he start with?
28. An article sells for 480 baht. This price gives the retailer a profit of 20 percent on her costs. What is the cost of this article?
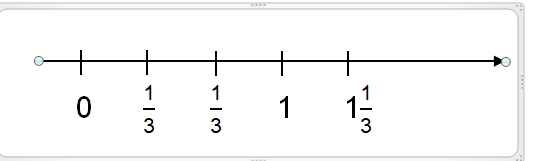
29. Marks are equally spaced on a number line as shown above How many marks would there be on this number line between the marks at 12 and 15?
30. It takes John 6 hours, reading at a constant rate, to read a certain book containing 240 pages of reading material. If Jack reads at twice this rate, how many minutes would it take him to read a book containing 120 pages of reading material?
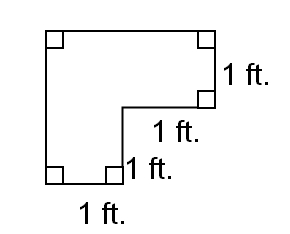
31. How many titles of the size and shape shown above are needed to completely cover a smallest square area?
32. If x2+ y2 = 2xy, then x must equal
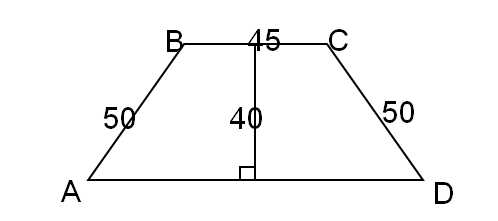
33. ABCD is a trapezoid where AB = 50, BC =45 and CD = 50. If the height of this trapezoid is equal to 40, find the length of AD.
34. If the sum of X and Y is equal to 200, and the average of Y and z is equal to 75, find X - Z.
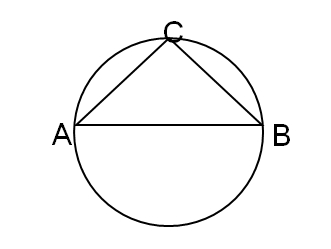
35. ABC is a triangle inside the circle where AB is diameter. If AC is equal to BC, find angle ABC.
36. In a group of 100 people, each person play football, basketball, both, or neither. 50 people play football, 75 people play basketball, and 15 people play neither football nor basketball. How many people in this group play both football and basketball?
37. A mixture of chemicals cost 300 baht per gallon. It is composed of chemical A that costs 400 baht per gallon and chemical B that costs 240 baht per gallon. In what ratio of Chemical A to chemical B mixed?
38. Mary has two bags, each one contains five white balls and five black balls. If a ball is drawn out of one bag and another ball is drawn out of another bag, what is the chance that at least one of the ball is white?
39. In the figure above shows a cylinder with radius 2 and height 5. If points A and B lie on the circumference of the top and bottom of the cylinder, respectively, what is the greatest possible straight line distance between A and B?
40. In the xy-plane, the line with equation y = 2x- 10 crosses the x - axis at the point with coordinates (a, b). What is the value of a?
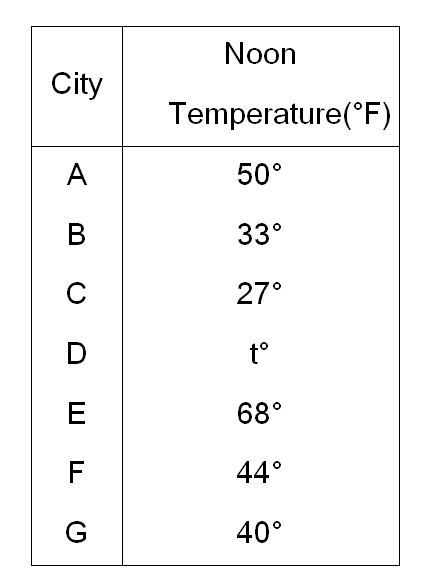
41. The table above show the noon temperature for seven cities designated A through G. If the median noon temperature of these cities is 40°F, then the noon temperature for City D could be any of the following except
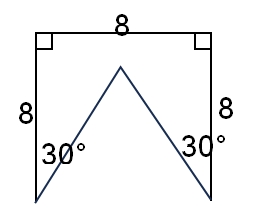
42. What is the perimeter of the figure above ?
43. If m is the greatest prime factor of 34 and n is the greatest prime factor of 50, what is the value of mn?
44. There are 50 students, 30 of the students play football, 25 of students play basketball and 15 of the students play both. If one student is picked randomly, what is the probability that it will be neither a football player nor a basketball player?
45. What is the measure of the central angle of the sector describing the percent of the assets in Stock?

46. How long is the shadow of a 35-foot tree, if a 98-foot tree casts a 42-foot shadow at the same time?
47. A rectangular field 50 meters in width and 120 meters in length is divided into two fields by a diagonal line. What is the length of fence (in meters) required to enclosed one of these fields?
48. In a shipment of 40 stereo components, only 80 percent of these parts were accepted as satisfactory. How many were not accepted in this shipment?
49. If k is the average of 10 and -14, then the average of k and -8 is
50. Which of the following is equal to a number greater than 1.
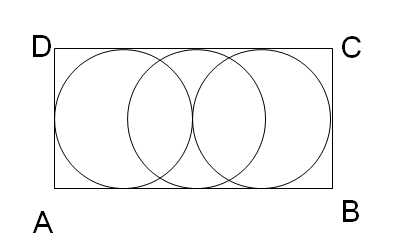
51. In the figure above, if the area of each of the circles enclosed in rectangle ABCD = 9π, then the area of the rectangle is
52. Which inequality is represented by the graph above?
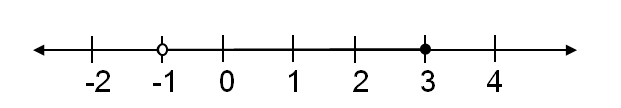
53. Examine the sales in this small neighborhood store. Which of the following combinations produce the largest sales?
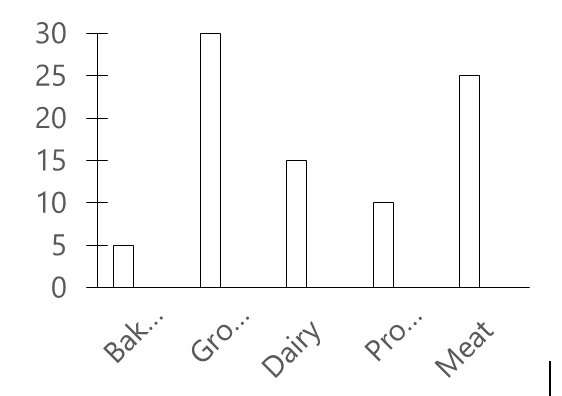
54. In the figure above, AE = 11, ED = 13, DC = 3 and CB = 2. What is the value of AB?
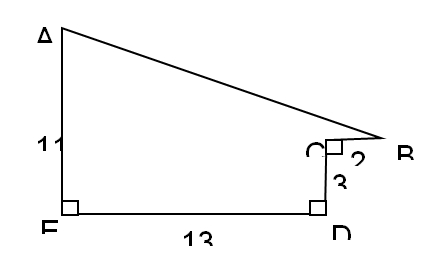
55. A 300,000 baht prize is to be divided among three people in the ratio of 2 : 3 : 5. What is the value of the smallest share?
CU AAT MATH
You got {{userScore}} out of {{maxScore}} correct
{{title}}
{{image}}
{{content}}

